Python 中的基本时间序列算法和统计假设

2020-05-15 08:00:00 · 飞浪

介绍时间序列算法广泛用于分析和预测基于时间的数据。这些算法建立在底层统计假设之上。在本指南中，您将学习统计假设和基本时间序列算法，以及它们在Python中的实现。让我们首先了解数据。

介绍

时间序列算法广泛用于分析和预测基于时间的数据。这些算法建立在底层统计假设之上。在本指南中，您将学习统计假设和基本时间序列算法，以及它们在 Python 中的实现。

让我们首先了解数据。

数据

在本指南中，您将使用一家连锁超市的虚构月销售数据，其中包含 564 个观测值和三个变量，如下所述：

date：每月的第一天
sales：每日销售额，以百万美元计
Class：表示训练和测试数据集划分的变量

下面的代码行导入所需的库和数据。

      import pandas as pd
import numpy as np 

# Reading the data
df = pd.read_csv("timeseries2.csv")
print(df.shape)
print(df.info())
    

输出：

      (564, 3)
    
    <class 'pandas.core.frame.DataFrame'>
    RangeIndex: 564 entries, 0 to 563
    Data columns (total 3 columns):
    date     564 non-null object
    sales    564 non-null float64
    Class    564 non-null object
    dtypes: float64(1), object(2)
    memory usage: 13.3+ KB
    None
    

下一步是创建用于模型验证的训练和测试数据集。您还将创建用于统计测试的训练数组。

      train = df[df["Class"] == "Train"]
test = df[df["Class"] == "Test"]
print(train.shape)
print(test.shape)

train_array = train["sales"]
print(train_array.shape)
    

输出：

      (552, 3)
    (12, 3)

    (552,)
    

准备好数据后，您就可以开始学习后续章节中的预测技术了。不过，在开始预测之前，了解时间序列中的白噪声和平稳性的统计概念非常重要。

白噪音

白噪声序列是纯随机的时间序列，其变量独立且分布相同，均值为零。这意味着观测值具有相同的方差，并且没有自相关性。

最初的技术之一是查看汇总统计数据。这可以通过以下代码完成。输出显示平均值不为零，标准差不为一。这些数字表明该序列不是白噪声。

      print(train_array.describe())

输出：

      count    552.000000
    mean       6.221014
    std        2.105854
    min        2.100000
    25%        5.000000
    50%        6.000000
    75%        6.900000
    max       12.300000
    Name: sales, dtype: float64
    

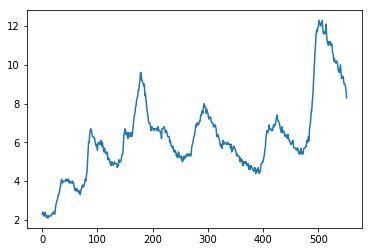
下一步是可视化该系列，可以使用下面的代码来完成。

      import matplotlib.pyplot as plt
train_array.plot()
plt.show()
    

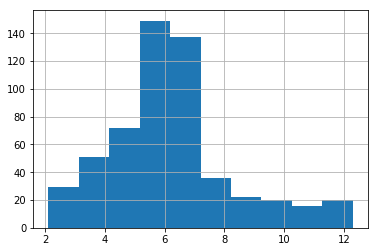
此可视化中的信息表明数据不是纯随机序列。您还可以创建直方图来确认分布是否正常。

      # histogram plot
train_array.hist()
plt.show()
    

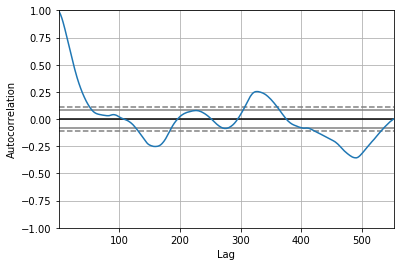
以上两个图都证实该序列不是白噪声。另一种确认方法是通过自相关，预计为零。可以使用下面的代码将其可视化。

      from pandas.plotting import autocorrelation_plot
autocorrelation_plot(train_array)
plt.show()
    

上面的输出显示出明显的自相关模式。以上所有分析都表明这不是白噪声序列。

文具系列

流行的时间序列算法之一是自回归综合移动平均法 (ARIMA)，它被定义为平稳序列。平稳序列是指其属性不会随时间而变化的序列。有几种方法可以检查序列的平稳性。这里要用到的是增强迪基-福勒检验法。

增强型迪基-福勒检验

增强型迪基-福勒检验是一种统计单位根检验。该检验使用自回归模型，并针对多个不同的滞后值优化信息标准。

检验的零假设是时间序列不是平稳的，而备择假设（拒绝零假设）是时间序列是平稳的。

第一步是从statsmodels包中导入adfuller模块。这在下面的第一行代码中完成。第二行使用训练数据集的sales变量创建一系列值。其余行进行测试并打印结果值。

      from statsmodels.tsa.stattools import adfuller

X = train.sales

result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))
    

输出：

      ADF Statistic: -2.960313
    p-value: 0.038771
    Critical Values:
    	1%: -3.442
    	5%: -2.867
    	10%: -2.570
    

上面的输出显示 p 值略低于阈值 0.05，这意味着您拒绝了原假设。该序列似乎大致平稳。了解了时间序列的基本统计概念后，您现在将构建时间序列预测模型。

构建模型之前的最后一步是创建一个将用作评估指标的效用函数。下面的代码创建了用于计算平均绝对百分比误差(MAPE) 的函数，这是要使用的指标。MAPE 值越低，预测模型性能越好。

      def mean_absolute_percentage_error(y_true, y_pred): 
    y_true, y_pred = np.array(y_true), np.array(y_pred)
    return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
    

简单指数平滑法

在指数平滑法中，预测是使用过去观测值的加权平均值得出的，权重随着观测值的变旧而呈指数衰减。水平的平滑参数值由参数smoothing_level决定。

下面的前两行代码导入了所需的库和模块。第三行拟合简单指数模型，而第四行生成测试数据的预测。最后，使用mean_absolute_percentage_error()函数生成测试数据的 MAPE 误差，结果为 10%。

      import statsmodels.api as sm
from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt

model1 = SimpleExpSmoothing(np.asarray(train['sales'])).fit(smoothing_level=0.7,optimized=False)

test['SimpleExp'] = model1.forecast(len(test))
mean_absolute_percentage_error(test.sales, test.SimpleExp)
    

输出：

      10.05

霍尔特线性趋势

这是简单指数平滑法的扩展，在生成预测时考虑了趋势成分。此方法涉及两个平滑方程，一个用于水平，一个用于趋势成分。

下面的代码行在训练数据上创建模型，在测试数据上生成预测，并使用效用函数评估模型性能。

      fit_holt = Holt(np.asarray(train['sales'])).fit(smoothing_level = 0.5,smoothing_slope = 0.1)

test['Holt_linear_model'] = fit_holt.forecast(len(test))

mean_absolute_percentage_error(test.sales, test.Holt_linear_model)

输出：

      2.15

上面的输出显示测试数据的 MAPE 为 2.1%。

Holt-Winters 方法

这是 holt-linear 模型的扩展，它在生成预测时同时考虑趋势和季节性成分。

下面的代码行在训练数据上创建模型，在测试数据上生成预测，并使用效用函数评估模型性能。

      fit_holt_winter = ExponentialSmoothing(np.asarray(train['sales']) ,seasonal_periods=6 ,trend='add', seasonal='add',).fit()

test['Holt_Winter'] = fit_holt_winter.forecast(len(test))

mean_absolute_percentage_error(test.sales, test.Holt_Winter)

输出：

      6.837

上面的输出显示测试数据的 MAPE 为 6.8%。

结论

在本指南中，您了解了时间序列数据中白噪声和平稳性的基本统计概念。您还学习了如何使用 Python 实现基本的时间序列预测模型。

模型在测试数据上的表现总结如下：

简单指数平滑：MAPE 为 10%
Holt 线性趋势模型：MAPE 为 2.1%
Holt-Winters 方法：MAPE 为 6.8%

简单指数平滑模型表现不错，平均绝对误差 (MAPE) 较低，为 10%。然而，其他两个模型表现更佳，平均绝对误差甚至更低。霍尔特线性趋势模型凭借最低的 2.1% 平均绝对误差脱颖而出。

要了解有关使用 Python 进行数据科学的更多信息，请参阅以下指南。

_{免责声明：本内容来源于第三方作者授权、网友推荐或互联网整理，旨在为广大用户提供学习与参考之用。所有文本和图片版权归原创网站或作者本人所有，其观点并不代表本站立场。如有任何版权侵犯或转载不当之情况，请与我们取得联系，我们将尽快进行相关处理与修改。感谢您的理解与支持！}

_查看原文

python

技术指南

阅读全文

Python 中的基本时间序列算法和统计假设

杭州电子商务研究院

4年前 · 面向社会、服务行业、政产学研结合、整合资源、和谐发展

(564, 3) <class 'pandas.core.frame.DataFrame'> RangeIndex: 564 entries, 0 to 563 Data columns (total 3 columns): date 564 non-null object sales 564 non-null float64 Class 564 non-null object dtypes: float64(1), object(2) memory usage: 13.3+ KB None

count 552.000000 mean 6.221014 std 2.105854 min 2.100000 25% 5.000000 50% 6.000000 75% 6.900000 max 12.300000 Name: sales, dtype: float64

from statsmodels.tsa.stattools import adfuller X = train.sales result = adfuller(X) print('ADF Statistic: %f' % result[0]) print('p-value: %f' % result[1]) print('Critical Values:') for key, value in result[4].items(): print('\t%s: %.3f' % (key, value))

import statsmodels.api as sm from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt model1 = SimpleExpSmoothing(np.asarray(train['sales'])).fit(smoothing_level=0.7,optimized=False) test['SimpleExp'] = model1.forecast(len(test)) mean_absolute_percentage_error(test.sales, test.SimpleExp)

fit_holt = Holt(np.asarray(train['sales'])).fit(smoothing_level = 0.5,smoothing_slope = 0.1) test['Holt_linear_model'] = fit_holt.forecast(len(test)) mean_absolute_percentage_error(test.sales, test.Holt_linear_model)

fit_holt_winter = ExponentialSmoothing(np.asarray(train['sales']) ,seasonal_periods=6 ,trend='add', seasonal='add',).fit() test['Holt_Winter'] = fit_holt_winter.forecast(len(test)) mean_absolute_percentage_error(test.sales, test.Holt_Winter)