RNN 入门

2020-09-09 08:00:00 · 飞浪

介绍循环神经网络(RNN)是一种流行的人工神经网络。RNN之所以被称为循环神经网络，是因为序列中每个元素的输出都依赖于之前的计算。当你看电影时，你会把各个点连起来，因为你知道最后几个

介绍

循环神经网络 (RNN) 是一种流行的人工神经网络。RNN 之所以被称为循环神经网络，是因为序列中每个元素的输出都依赖于之前的计算。

当你看电影时，你会把各个点连起来，因为你知道最后几个场景发生了什么。传统的 NN 架构无法做到这一点。它们无法使用之前的场景来预测下一个场景会发生什么。因此，为了解决与序列相关的问题，人们使用了 RNN。

本教程将简要介绍简单的 RNN 和多层感知器 (MLP) 的概念。您将在时间序列数据集上构建模型来预测 B 值。在此处下载数据。

理解 MLP

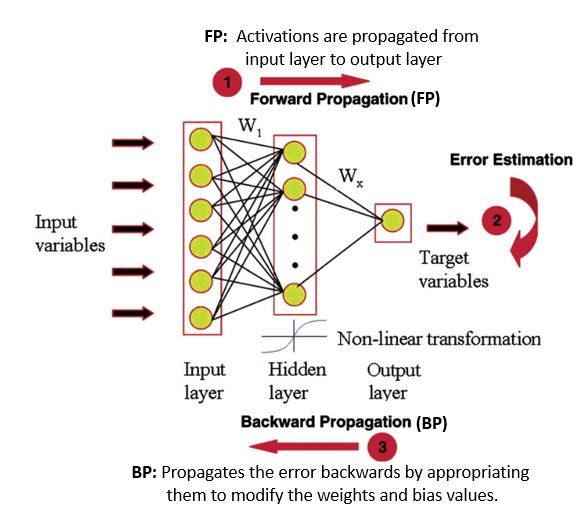
MLP 是一种前馈神经网络。它由三个节点组成：输入层、隐藏层和输出层。它们是完全连接的，因为一层中的每个节点都以一定的权重连接到下一层中的每个节点。MLP 使用前向传播，然后使用称为反向传播的监督学习技术进行训练。MLP 的表示如下所示。

图片来源：Mashallah Rahimi

如果您有兴趣了解有关反向传播的更多信息，请参阅这篇博客文章。

理解简单的 RNN

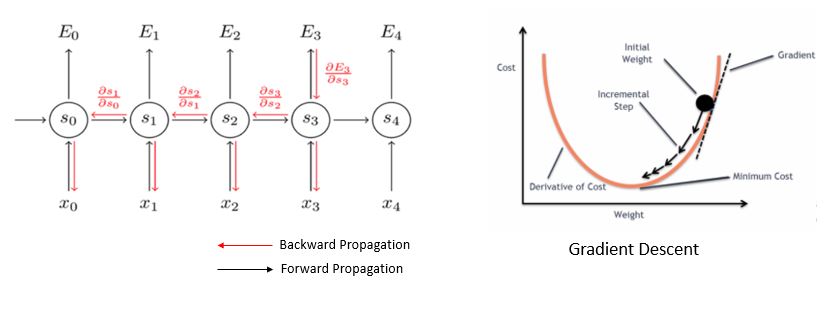
RNN 背后的理念是利用顺序信息。下图左侧是递归关系的图形说明。右侧部分说明了网络如何在长度为k的序列上随时间展开。典型的展开 RNN 如下所示：

图片来源：researchgate.net

该任务的最佳参数是U=W=1。让我们训练 RNN 模型。

理解随时间反向传播 (BPTT) 和消失梯度

图片来源：Pranjal Kumar

为了训练 RNN，我们使用了 BPTT。术语“反向传播”后面附加了“随时间变化”一词，以表明该算法应用于时间神经模型 (RNN)。BPTT 的任务是找到局部最小值，即误差最小的点。通过调整权重值，网络可以达到最小值。这个过程称为梯度下降。梯度（步骤）由导数、偏导数和链式法则计算得出。

但是 BPTT 很难学习长期依赖关系。您可能会建议添加更多 RNN。从理论上讲，这是正确的，但实际上却恰恰相反。RNN 的堆叠会导致梯度消失问题。BPTT 会使梯度变得非常小，从而有效地阻止权重改变其值，从而完全阻止 NN 进一步训练。

让我们实现代码。

代码实现

您将使用 Bicton 数据，使用 60 个数据点来预测第 61 个数据点。

      import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
import warnings
from sklearn.metrics import mean_absolute_error
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout,Flatten
warnings.filterwarnings("ignore")
    

添加日期列并将时间戳列转换为日期形式。

      bit_data=pd.read_csv("../input/bitstampUSD.csv")
bit_data["date"]=pd.to_datetime(bit_data["Timestamp"],unit="s").dt.date
group=bit_data.groupby("date")
data=group["Close"].mean()
    

      data.shape

目标是预测每日收盘数据。最后 60 行被视为测试数据集。

      close_train=data.iloc[:len(data)-60]
close_test=data.iloc[len(close_train):]
    

此处的值设置在 0-1 之间，以避免高值占主导地位。

      close_train=np.array(close_train)
close_train=close_train.reshape(close_train.shape[0],1)
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
close_scaled=scaler.fit_transform(close_train)
    

选择 60 个数据点作为 x-train，第 61 个数据点作为 y-train。

      timestep=60
x_train=[]
y_train=[]

for i in range(timestep,close_scaled.shape[0]):
    x_train.append(close_scaled[i-timestep:i,0])
    y_train.append(close_scaled[i,0])

x_train,y_train=np.array(x_train),np.array(y_train)
x_train=x_train.reshape(x_train.shape[0],x_train.shape[1],1) #reshaped for RNN
print("x-train-shape= ",x_train.shape)
print("y-train-shape= ",y_train.shape)
    

MLP 的实施

Keras 的sequation() API 用于创建模型。MLP 建立在密集连接的层堆栈上。因此，添加了dense()函数来提取重要参数。第一层有 16 个输出神经元，下一层有 8 个输出。两者都使用 ReLU 激活。

接下来，通过调整超参数来编译架构。这里，优化器用于优化我们的模型和损失函数。然后，使用 50 个时期或迭代将训练数据拟合到模型中。

      model = Sequential()
model.add(Dense(56, input_shape=(x_train.shape[1],1), activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Flatten())
model.add(Dense(1)

model.compile(optimizer="adam",loss="mean_squared_error")
model.fit(x_train,y_train,epochs=50,batch_size=64)
    

现在已经准备好测试数据以供预测。

      inputs=data[len(data)-len(close_test)-timestep:]
inputs=inputs.values.reshape(-1,1)
inputs=scaler.transform(inputs)
    

      x_test=[]
for i in range(timestep,inputs.shape[0]):
    x_test.append(inputs[i-timestep:i,0])
x_test=np.array(x_test)
x_test=x_test.reshape(x_test.shape[0],x_test.shape[1],1)
    

让我们将该模型应用到测试数据上。

      predicted_data=model.predict(x_test)
predicted_data=scaler.inverse_transform(predicted_data)
    

      data_test=np.array(close_test)
data_test=data_test.reshape(len(data_test),1)
    

绘制预测图。

      plt.figure(figsize=(8,4), dpi=80, facecolor='w', edgecolor='k')
plt.plot(data_test,color="r",label="true result")
plt.plot(predicted_data,color="b",label="predicted result")
plt.legend()
plt.xlabel("Time(60 days)")
plt.ylabel("Values")
plt.grid(True)
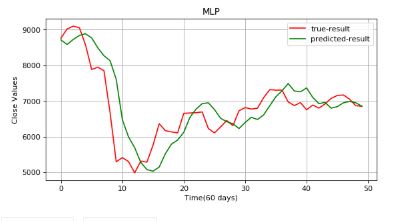
plt.show()
    

真实值和预测结果差距很大，结果不可靠，我们来实现 RNN 吧。

简单 RNN 的实现

SimpleRNN将具有形状为 (batch_size, internal_units) 的 2D 张量和relu的激活函数。如前所述，RNN 通过隐藏状态传递信息，因此我们保持真实。每层之后都会添加一个 dropout 层。矩阵将使用Flatten()转换为一列。最后，编译模型。

      reg=Sequential()
reg.add(SimpleRNN(128,activation="relu",return_sequences=True,input_shape=(x_train.shape[1],1)))
reg.add(Dropout(0.25))
reg.add(SimpleRNN(256,activation="relu",return_sequences=True))
reg.add(Dropout(0.25))
reg.add(SimpleRNN(512,activation="relu",return_sequences=True))
reg.add(Dropout(0.35))
reg.add(Flatten())
reg.add(Dense(1))

reg.compile(optimizer="adam",loss="mean_squared_error")
reg.fit(x_train,y_train,epochs=50,batch_size=64)
    

现在该进行预测了。

      predicted_data=reg.predict(x_test)
predicted_data=scaler.inverse_transform(predicted_data)
    

      plt.figure(figsize=(8,4), dpi=80, facecolor='w', edgecolor='k')
plt.plot(data_test,color="r",label="true-result")
plt.plot(predicted_data,color="g",label="predicted-result")
plt.legend()
plt.xlabel("Time(60 days)")
plt.ylabel("Close Values")
plt.grid(True)
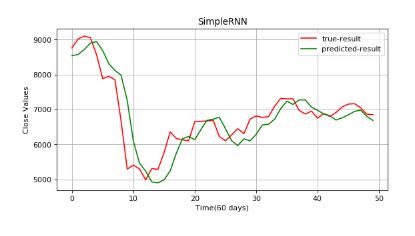
plt.show()
    

结果仍然不令人满意。这是由于信息消失（梯度消失）造成的。阅读有关长短期记忆 (LTSM)和门控循环单元 (GRU) 的这些附加指南，以了解有关它们如何在 RNN 上构建并解决此问题的更多信息。

结论

输出之间仍然存在相当大的滞后。有几种方法可以解决消失梯度问题，其中一种是门控。门控决定何时忘记当前输入以及何时记住它以供将来的时间步骤使用。目前最流行的门控类型是 LSTM 和 GRU。

您可以使用您选择的其他数据尝试上述模型。我建议更改一些超参数值并更改层数，并注意结果的差异。

欢迎随时在Codealphabet向我提问。

_{免责声明：本内容来源于第三方作者授权、网友推荐或互联网整理，旨在为广大用户提供学习与参考之用。所有文本和图片版权归原创网站或作者本人所有，其观点并不代表本站立场。如有任何版权侵犯或转载不当之情况，请与我们取得联系，我们将尽快进行相关处理与修改。感谢您的理解与支持！}

_查看原文

技术指南

阅读全文

RNN 入门

杭州电子商务研究院

4年前 · 面向社会、服务行业、政产学研结合、整合资源、和谐发展

import numpy as np import pandas as pd import matplotlib.pyplot as plt import warnings from sklearn.metrics import mean_absolute_error from keras.models import Sequential from keras.layers import Dense, LSTM, Dropout,Flatten warnings.filterwarnings("ignore")

close_train=np.array(close_train) close_train=close_train.reshape(close_train.shape[0],1) from sklearn.preprocessing import MinMaxScaler scaler=MinMaxScaler(feature_range=(0,1)) close_scaled=scaler.fit_transform(close_train)

timestep=60 x_train=[] y_train=[] for i in range(timestep,close_scaled.shape[0]): x_train.append(close_scaled[i-timestep:i,0]) y_train.append(close_scaled[i,0]) x_train,y_train=np.array(x_train),np.array(y_train) x_train=x_train.reshape(x_train.shape[0],x_train.shape[1],1) #reshaped for RNN print("x-train-shape= ",x_train.shape) print("y-train-shape= ",y_train.shape)

model = Sequential() model.add(Dense(56, input_shape=(x_train.shape[1],1), activation='relu')) model.add(Dense(32, activation='relu')) model.add(Flatten()) model.add(Dense(1) model.compile(optimizer="adam",loss="mean_squared_error") model.fit(x_train,y_train,epochs=50,batch_size=64)

plt.figure(figsize=(8,4), dpi=80, facecolor='w', edgecolor='k') plt.plot(data_test,color="r",label="true result") plt.plot(predicted_data,color="b",label="predicted result") plt.legend() plt.xlabel("Time(60 days)") plt.ylabel("Values") plt.grid(True) plt.show()

reg=Sequential() reg.add(SimpleRNN(128,activation="relu",return_sequences=True,input_shape=(x_train.shape[1],1))) reg.add(Dropout(0.25)) reg.add(SimpleRNN(256,activation="relu",return_sequences=True)) reg.add(Dropout(0.25)) reg.add(SimpleRNN(512,activation="relu",return_sequences=True)) reg.add(Dropout(0.35)) reg.add(Flatten()) reg.add(Dense(1)) reg.compile(optimizer="adam",loss="mean_squared_error") reg.fit(x_train,y_train,epochs=50,batch_size=64)

plt.figure(figsize=(8,4), dpi=80, facecolor='w', edgecolor='k') plt.plot(data_test,color="r",label="true-result") plt.plot(predicted_data,color="g",label="predicted-result") plt.legend() plt.xlabel("Time(60 days)") plt.ylabel("Close Values") plt.grid(True) plt.show()