RNN 中的 LSTM 单元简介
介绍
长短期记忆
LSTM(长短期记忆的缩写)主要解决反向传播中的梯度消失问题。LSTM 使用门控机制来控制记忆过程。LSTM 中的信息可以通过打开和关闭的门来存储、写入或读取。这些门以模拟格式存储记忆,通过 0-1 之间的 S 形函数实现元素级乘法。模拟本质上是可微分的,适用于反向传播。
让我们看一下 LSTM 的架构。
双曲函数
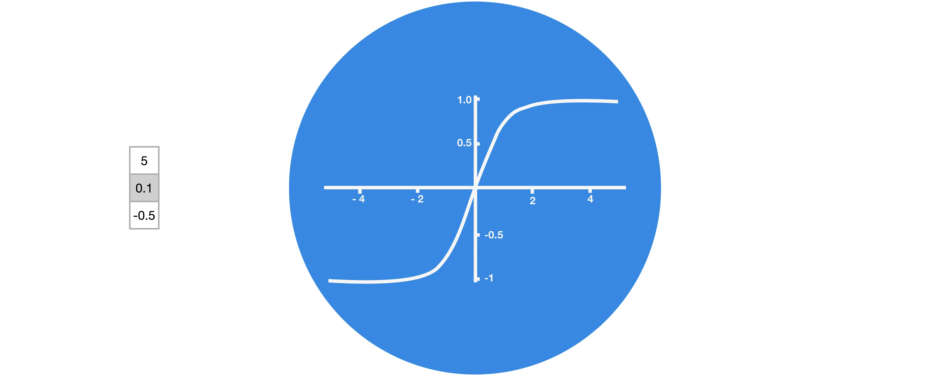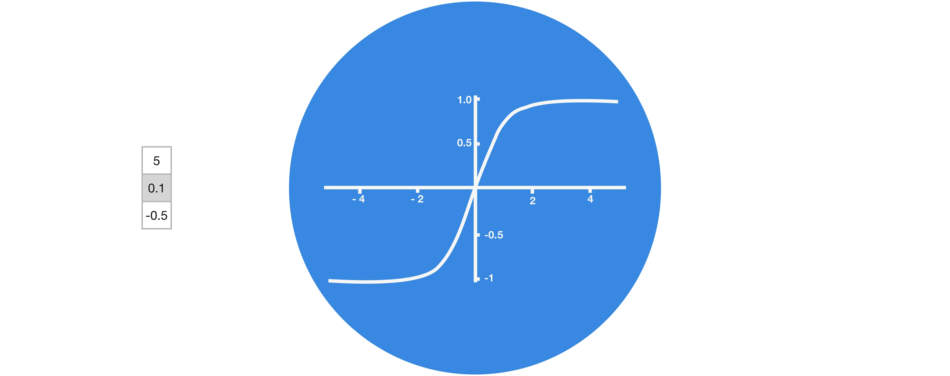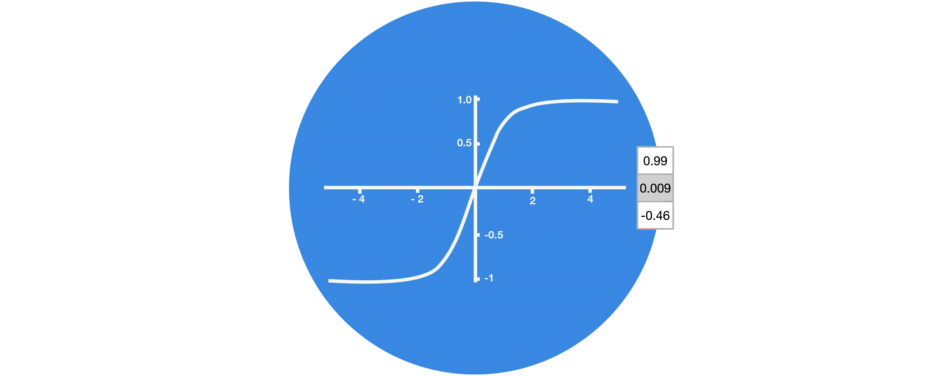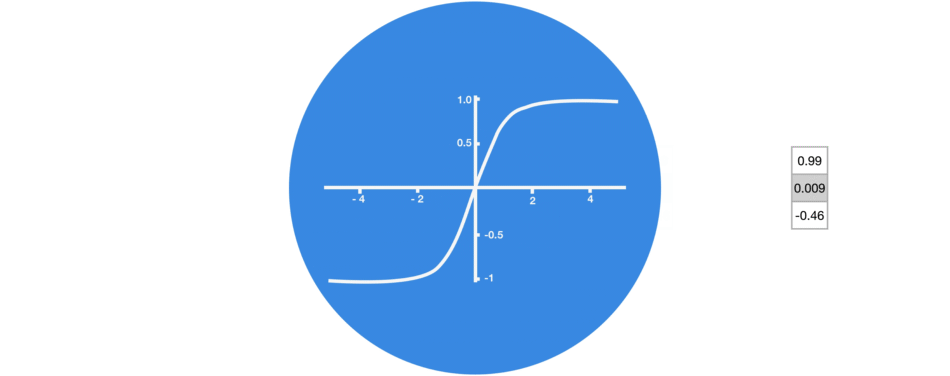
Tanh 是一种非线性激活函数。它调节流经网络的值,将值保持在 -1 和 1 之间。为了避免信息衰减,需要一个二阶导数可以存活更长时间的函数。可能存在某些值变得非常大的情况,从而进一步导致值变得微不足道。您可以看到值 5 是如何由于该函数而保持在边界之间的。
乙状结肠
Sigmoid 属于非线性激活函数家族。它包含在门中。与 tanh 不同,sigmoid 将值保持在 0 到 1 之间。它帮助网络更新或忘记数据。如果乘法结果为 0,则认为信息被遗忘。同样,如果值为 1,则信息保留。
这将帮助网络了解哪些数据可以被遗忘以及哪些数据值得保留。
忘记门
遗忘门决定哪些信息需要注意,哪些可以忽略。当前输入 X(t) 和隐藏状态 h(t-1) 的信息通过 S 型函数传递。S 型函数生成 0 到 1 之间的值。它判断旧输出的部分是否必要(通过使输出更接近 1)。f(t) 的这个值稍后将被单元用于逐点乘法。
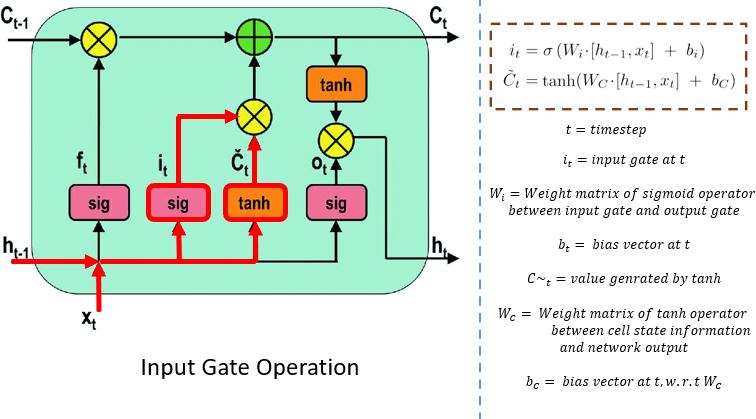
输入门
输入门执行以下操作来更新细胞状态。
首先,将当前状态 X(t) 和先前的隐藏状态 h(t-1) 传入第二个 sigmoid 函数。值在 0(重要)和 1(不重要)之间变换。
接下来,隐藏状态和当前状态的相同信息将通过 tanh 函数。为了调节网络,tanh 运算符将创建一个向量 (C~(t) ),其中包含 -1 和 1 之间的所有可能值。激活函数生成的输出值已准备好进行逐点乘法。
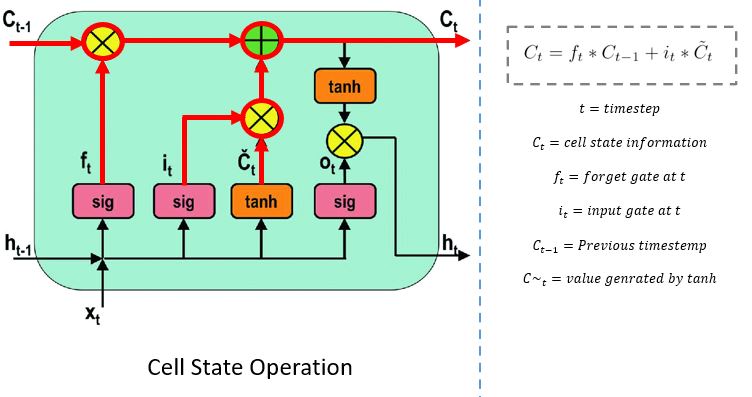
细胞状态
网络拥有来自遗忘门和输入门的足够信息。下一步是决定并将新状态的信息存储在单元状态中。前一个单元状态 C(t-1) 与遗忘向量 f(t) 相乘。如果结果为 0,则单元状态中的值将被删除。接下来,网络获取输入向量 i(t) 的输出值并执行逐点加法,从而更新单元状态,为网络提供新的单元状态 C(t)。
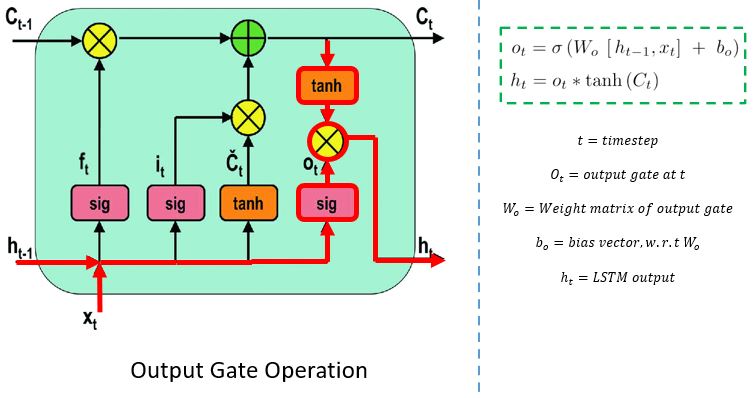
输出门
输出门决定下一个隐藏状态的值。此状态包含有关先前输入的信息。
首先,将当前状态和先前隐藏状态的值传入第三个 S 型函数。然后,将从单元状态生成的新单元状态传入 tanh 函数。这两个输出逐点相乘。根据最终值,网络决定隐藏状态应携带哪些信息。此隐藏状态用于预测。
最后,新的细胞状态和新的隐藏状态被延续到下一个时间步骤。
总而言之,遗忘门决定需要先前步骤中的哪些相关信息。输入门决定可以从当前步骤添加哪些相关信息,输出门确定下一个隐藏状态。
让我们实现代码。
代码实现
注意: *在构建 LSTM 模型之前,请参考上一个教程中导入重要库和数据预处理的代码。*
从 Keras Layers API 中导入了诸如LSTM层、正则化层dropout和核心层density等重要类。
在第一层中,输入为 50 个单位,return_sequence保持为true,因为它将返回维度为 50 的向量序列。由于下一层的 return_sequence 为False,因此它将返回维度为 100 的单个向量。
from sklearn.metrics import mean_absolute_error
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout
modell = Sequential()
modell.add(LSTM(50, return_sequences=True, input_shape=(x_train.shape[1],1)))
modell.add(Dropout(0.2))
modell.add(LSTM(100, return_sequences=False))
modell.add(Dropout(0.2))
modell.add(Dense(1))
modell.compile(loss="mean_squared_error",optimizer="rmsprop")
modell.fit(x_train,y_train,epochs= 50,batch_size=64)
现在已经准备好测试数据以供预测。
inputs=data[len(data)-len(close_test)-timestep:]
inputs=inputs.values.reshape(-1,1)
inputs=scaler.transform(inputs)
x_test=[]
for i in range(timestep,inputs.shape[0]):
x_test.append(inputs[i-timestep:i,0])
x_test=np.array(x_test)
x_test=x_test.reshape(x_test.shape[0],x_test.shape[1],1)
让我们将该模型应用于测试数据。
predicted_data=modell.predict(x_test)
predicted_data=scaler.inverse_transform(predicted_data)
data_test=np.array(close_test)
data_test=data_test.reshape(len(data_test),1)
預測時間。
plt.figure(figsize=(8,4), dpi=80, facecolor='w', edgecolor='k')
plt.plot(data_test,color="r",label="true-result")
plt.plot(predicted_data,color="g",label="predicted-result")
plt.legend()
plt.title("LSTM")
plt.xlabel("Time(60 days)")
plt.ylabel("Close Values")
plt.grid(True)
plt.show()
结论
LSTM 优于 SimpleRNN 和 MLP!
结果是可以接受的,因为真实结果和预测结果几乎一致。在处理顺序数据时,RNN 是一个不错的选择,但它们存在短期记忆问题。引入门控机制可以调节 RNN 中的信息流并缓解该问题。
我建议更改超参数的值或使用不同的优化器集(例如 Adam、SDG 等)编译模型,以查看图中的变化。您还可以增加 LSTM 网络中的层数并检查结果。您可以随意将此模型与任何其他数据集一起使用。
本指南简要介绍了 LSTM 中涉及的门控技术,并使用 Keras API 实现了该模型。现在您已经了解了 LSTM 的工作原理,下一篇指南将介绍门控循环单元 (GRU),这是 LSTM 的修改版本,使用更少的参数和输出状态。
免责声明:本内容来源于第三方作者授权、网友推荐或互联网整理,旨在为广大用户提供学习与参考之用。所有文本和图片版权归原创网站或作者本人所有,其观点并不代表本站立场。如有任何版权侵犯或转载不当之情况,请与我们取得联系,我们将尽快进行相关处理与修改。感谢您的理解与支持!








































请先 登录后发表评论 ~