使用 R 进行多项式函数分析
介绍
当特征点几乎排列成一条直线时,您可以使用简单线性回归或多元线性回归(在有多个特征点的情况下)。但是,如何将函数拟合到点为非线性的特征上?在本指南中,您将学习如何实现适用于非线性点的多项式函数。您将使用 R 进行工作,并且应该已经具备回归的基本知识。
描述原始数据并创建训练和测试数据
原始数据
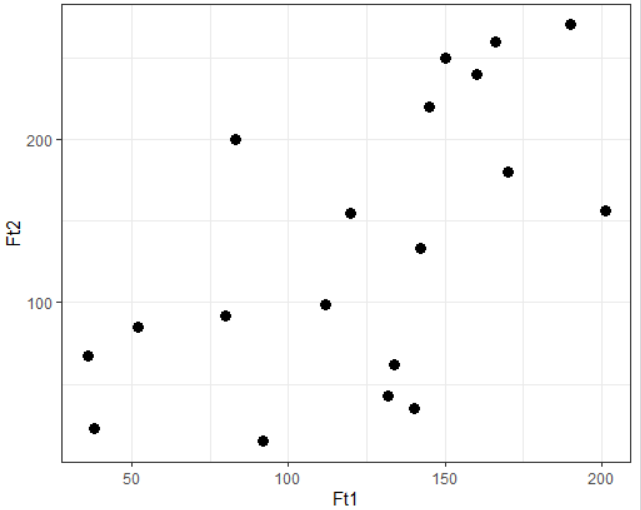
考虑一个因变量 Ft1 和一个自变量 Ft2,它们有 19 个数据点,如下所示:
| FT1 | 財產夾 |
|---|---|
| 三十八 | 23 |
| 52 | 85 |
| 三十六 | 67 |
| 92 | 15 |
| 83 | 200 |
| 170 | 180 |
| 140 | 三十五 |
| 201 | 156 |
| 112 | 99 |
| 132 | 43 |
| 80 | 92 |
| 134 | 62 |
| 150 | 250 |
| 160 | 240 |
| 190 | 270 |
| 145 | 220 |
| 166 | 260 |
| 120 | 155 |
| 142 | 133 |
您可以使用ggplot2库可视化完整的数据,如下所示:
# Load ggplot2 library
library(ggplot2)
# Load data from a CSV file
data <- read.csv("file.csv")
# Visualize the data
ggplot(data) +
geom_point(aes(Ft1, Ft2),size=3) +
theme_bw()
创建训练和测试数据
您可以使用以下代码将原始数据按照 75:25 的比例分成训练和测试:
# Set a seed value for reproducible results
set.seed(70)
# Split the data
ind <- sample(x = nrow(data), size = floor(0.75 * nrow(data)))
# Store the value in train and test dataframes
train <- data[ind,]
test <- data[-ind,]
建立不同次数的多项式回归
要在 R 中建立多项式回归,请从lm函数开始,然后调整公式参数值。您必须知道,多项式函数的“次数”必须小于唯一点的数量。
此时,训练数据框中只有 14 个数据点,因此可以拥有的最大多项式次数为 13。给定的代码构建了四个次数分别为 1、3、5 和 9 的多项式函数。
# Order 1
poly_reg1 <- lm(formula = Ft1~poly(Ft2,1),
data = train)
# Order 3
poly_reg3 <- lm(formula = Ft1~poly(Ft2,3),
data = train)
# Order 5
poly_reg5 <- lm(formula = Ft1~poly(Ft2,5),
data = train)
# Order 9
poly_reg9 <- lm(formula = Ft1~poly(Ft2,9),
data = train)
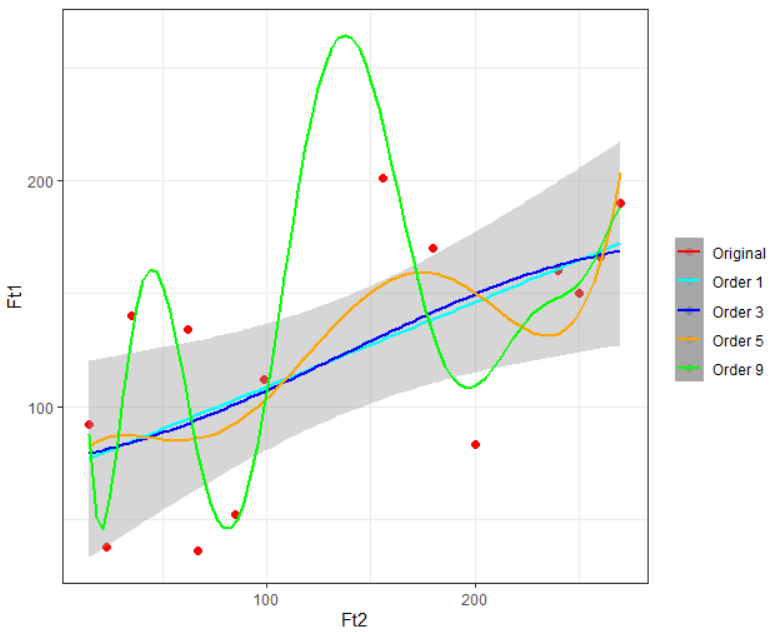
成功构建这四个模型后,您可以使用给定的ggplot代码在训练数据上将它们可视化:
ggplot(train) +
geom_point(aes(Ft2, Ft1, col = "Original"), cex = 2) +
stat_smooth(method = "lm", formula = y~poly(x,1), aes(Ft2, poly_reg1$fitted.values, col = "Order 1")) +
stat_smooth(method = "lm", formula = y~poly(x,3), aes(Ft2, poly_reg3$fitted.values, col = "Order 3")) +
stat_smooth(method = "lm", formula = y~poly(x,5), aes(Ft2, poly_reg5$fitted.values, col = "Order 5")) +
stat_smooth(method = "lm", formula = y~poly(x,9), aes(Ft2, poly_reg9$fitted.values, col = "Order 9")) +
scale_colour_manual("",
breaks = c("Original", "Order 1", "Order 3", "Order 5", "Order 9"),
values = c("red","cyan", "blue","orange","green")) +
theme_bw()
测量训练和测试数据的 RSS 值
您拥有获取训练数据 RSS 值的所有信息,但要获取测试数据的 RSS 值,您需要预测 Ft1 值。使用给定的代码来执行此操作:
# Predicting values using test data by each model
poly1_pred <- predict(object = poly_reg1,
newdata = data.frame(Ft2 = test$Ft2))
poly3_pred <- predict(object = poly_reg3,
newdata = data.frame(Ft2 = test$Ft2))
poly5_pred <- predict(object = poly_reg5,
newdata = data.frame(Ft2 = test$Ft2))
poly9_pred <- predict(object = poly_reg9,
newdata = data.frame(Ft2 = test$Ft2))
现在,您可以找到两条数据的 RSS 值,如下所示:
# RSS for train data based on each model
train_rss1 <- mean((train$Ft1 - poly_reg1$fitted.values)^2) # Order 1
train_rss3 <- mean((train$Ft1 - poly_reg3$fitted.values)^2) # Order 3
train_rss5 <- mean((train$Ft1 - poly_reg5$fitted.values)^2) # Order 5
train_rss9 <- mean((train$Ft1 - poly_reg9$fitted.values)^2) # Order 9
# RSS for test data based on each model
test_rss1 <- mean((test$Ft1 - poly1_pred)^2) # Order 1
test_rss3 <- mean((test$Ft1 - poly3_pred)^2) # Order 3
test_rss5 <- mean((test$Ft1 - poly5_pred)^2) # Order 5
test_rss9 <- mean((test$Ft1 - poly9_pred)^2) # Order 9
| 训练RSS1 | 训练RSS3 | 训练RSS5 | 训练RSS9 |
|---|---|---|---|
| 0.000 | 1673.867 | 1405.703 | 4 |
免责声明:本内容来源于第三方作者授权、网友推荐或互联网整理,旨在为广大用户提供学习与参考之用。所有文本和图片版权归原创网站或作者本人所有,其观点并不代表本站立场。如有任何版权侵犯或转载不当之情况,请与我们取得联系,我们将尽快进行相关处理与修改。感谢您的理解与支持!






































请先 登录后发表评论 ~